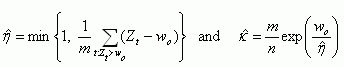
Consider the problem of verifying deterministic forecasts of a binary event when the event is rare. The standard approach is to record the frequencies with which the event was observed and forecasted in a two-by-two table, and then to quantify forecast quality with summary measures of the table. The frequency with which rare events are observed may be low, which increases sampling variation in such measures and creates uncertainty about forecast quality. Most measures also necessarily degenerate to trivial values as event rarity increases, which projects misleading impressions of forecast quality and complicates the discrimination between forecasting systems. These problems can be overcome by constructing a probability model for how the entries in the table are expected to change as rarity increases. The model proposed here identifies two, key parameters for describing such changes and places parametric constraints on the table that help to reduce sampling variation.
Suppose that the event is forecasted when a continuous, scalar quantity X exceeds a threshold u, and that the event is observed when a continuous, scalar quantity Y exceeds a threshold v. The two-by-two table is then defined by three probabilities: Pr(X > u), Pr(Y > v), and the joint probability Pr(X > u, Y > v). Suppose also that the forecast threshold u is chosen so that Pr(X > u) = Pr(Y > v) = p for all base rates p. This simplification means that the probability model will only describe the quality of forecasts were they to be perfectly calibrated. It remains to define the joint probability. Results from extreme-value theory imply that Pr( X > u, Y > v) = κp1/η when p is small under mild conditions on the joint distribution of X and Y, where κ and η are unspecified parameters satisfying κ > 0 and 0 < η ≤ 1. These two parameters therefore define the two-by-two table, and so forecast performance, for any small base rate p. The particular values of κ and η depend on the quality of the forecasts and need to be estimated from data. Once they are estimated, however, the model can be used to construct the table for any small base rate, and summary measures can be derived. For example, the hit rate is the proportion of observed events that are correctly forecasted, and is modelled by Pr(X > u, Y > v) / Pr(Y > v) = κp1/η-1. Plotting the estimated values of κ and η against each other for different forecasting systems is a useful way of comparing their abilities to forecast extreme events.
Estimating κ and η is computationally easy but
requires
care. Since the
model holds for only small values of p, a threshold base rate
p0 must
be chosen below which the model is considered to be a sufficiently
accurate description of the data. The parameters are then estimated
from those data for which both X
and Y exceed their upper p0-quantiles.
Once this
subset is chosen, analytical expressions for the maximum-likelihood
estimators are available. If {(Xt, Yt)
: t = 1,..., n} denotes the historical record of
X and Y variables then the estimators are
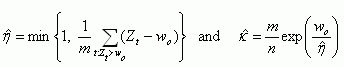
where w0 = -log p0,
m is the number
of Zt exceeding w0,
and
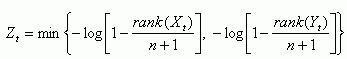
Choosing p0 involves a trade-off because larger p0 admit more data, increasing the precision of estimates, but reduce the accuracy of the probability model. The validity of the model assumptions should also be challenged with understanding of the physical processes generating the data, and the fit of the model should be assessed empirically with diagnostic plots and tests.
A more detailed description of the model, its assumptions and application, and examples of its use are given by Ferro (2007). Computer code written in the statistical programming language R is also available at http://www.secamlocal.ex.ac.uk/people/staff/ferro/Publications/xverif.r.
References
Ferro, C.A.T., 2007: A probability model for verifying deterministic
forecasts of extreme events. Wea. Forecasting, 22, 1089-1100.