Verifying probability of precipitation

Verifying probability of precipitation - an example from Finland

24-hour and 48-hour forecasts of probability of precipitation were made by the Finnish Meteorological Institute (FMI) during 2003, for daily precipitation in the city of Tampere in south central Finland. Three precipitation categories were used:
    Category 0:   RR ≤ 0.2 mm
    Category 1:   0.3 mm ≤ RR ≤ 4.4 mm
    Category 2:   RR ≥ 4.5 mm
The probability of rain in each category was predicted each day, with the probabilities across the three categories adding up to 1. Click here to view the data.

It is possible to verify these probabilistic forecasts using a variety of verification plots and statistics. Recall that verification of probability forecasts requires many samples in order to assess forecast quality, as it is not possible to say whether a single probability forecast (say, 30%) is right or wrong for a single outcome. The Tampere dataset gives forecasts for 365 days (actually a bit fewer since some days were missing), which is quite adequate for verifying probability forecasts.

First consider the probability of precipitation (POP), where "no precipitation" corresponds to Category 0, and "precipitation" corresponds to Categories 1 and 2 put together. This effectively treats the multi-category forecast like a forecast for a binary event. We can also consider the probablity of precipitation in the highest category (POP_hi) by taking "not heavier precipitation" to correspond to Categories 0 and 1, and "heavier precipitation" to correspond to Category 2.

The Brier score measures the mean squared probability error. It can be decomposed into three terms, where the first term measures the reliability (this term should be small for good forecasts), the second term measures the resolution (this term should be large for good forecasts, and is subtracted), and the third term measures the climatological uncertainty (independent of the forecast quality). For the Tampere forecasts the values of these quantities were:

	24-hour forecasts		48-hour forecasts
	POP	POP_hi	POP	POP_hi
Brier score	0.144	0.037	0.178	0.044
Reliability	0.025	0.003	0.027	0.003
Resolution	0.060	0.020	0.036	0.011
Uncertainty	0.179	0.054	0.187	0.052
Brier skill score	0.194	0.312	0.047	0.146

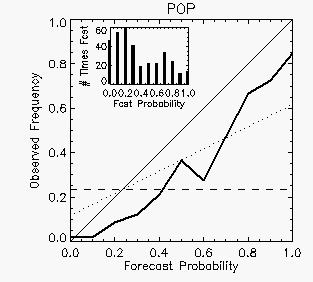The Brier score had lower values for the 24-hour forecasts than for the 48-hour forecasts, which means that the 24-hour forecasts were more accurate. The difference was due mainly to the 24-hour forecasts having better resolution (i.e., they were better at separating "precipitation " from "no precipitation"). The differences in the uncertainties between the 24- and 48-hour forecasts relate to different days having missing data - for a complete dataset these values would be identical. The POP_hi forecasts were more accurate than the POP forecasts. This is partly because heavier rainfall was rarer and the Brier score is heavily influenced by the no-event cases. To account for the relative frequency or rarity of events, the skill of the forecast relative to the sample climatology is often reported. The values of Brier skill score shown in the bottom row of the table show that the 24-hour forecasts for heavier rainfall occurrence were more skillful than for lighter rainfall or the longer forecast period.

The reliability of the forecasts, that is, the degree to which the forecast probabilities match the observed frequencies, can be assessed using a reliability diagram. The reliability of the 24-hour POP forecasts is shown by the heavy line in the diagram at left. If the forecasts had perfect reliability (i.e., no bias) this curve would lie along the diagonal 1:1 line. The dashed horizontal line shows the climatological frequency, and the dotted line midway between the 1:1 line and the horizontal denotes no skill relative to climatology. The location of the reliability curve to the right of the diagonal indicates that the probabilities were overestimated for all but the zero-probability cases, and only for the higher probability categories did the POP forecasts have more skill than climatology. The bar chart in the upper left of the plot shows the number of times each probability value was predicted.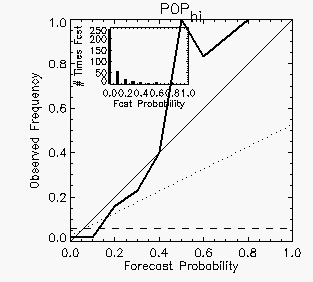

reliability diagram for heavier rain

The reliability diagram for the 24-hour POP_hi forecasts (right) shows a reliability curve much closer to the diagonal at low probabilities, but veering sharply away for probabilities of 0.5 or greater. However, these higher probabilities were rarely forecast (only eight forecasts of POP_hi equal to 0.5 or more) so the reliability curve is noisy because of undersampling. (In practice it is a good idea to plot data only when there are enough samples.)

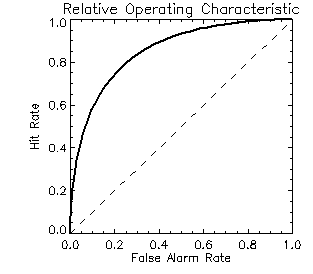The Relative Operating Characteristic (ROC) is often used to measure how well the probabilistic forecasts discriminate between events and non-events (resolution). Because it is independent of bias it can be viewed as a kind of potential skill. The ROC curve for 24-hour POP forecasts is shown here.

A forecast that discriminates perfectly would have a ROC curve that starts in the lower left and follows the y-axis (false alarm rate=0) up to the top left corner, then follows the top axis (hit rate=1) to the upper right corner. The area under the ROC curve is a scalar measure that is frequently used to summarize the resolution. The perfect value is 1.0 and the no-skill value is 0.5. For the Tampere forecasts the following ROC areas are obtained using both a simple trapezoid method and a curve-fitting method (preferred) to estimate the area under the curve:

	24-hour forecasts		48-hour forecasts
	POP	POP_hi	POP	POP_hi
ROC area (trapezoid rule)	0.857	0.849	0.767	0.763
ROC area (curve fitting)	0.855	0.870	0.771	0.785

These ROC areas suggest that the forecasts were able to resolve lighter and heavier rainfall with about the same ability. This similarity in the potential skill was not readily obvious from the Brier score, partly due to the bias in the POP forecasts.

Another diagnostic that is related to forecast resolution, but puts the performance into a decision-making context, is the relative value. This measures the usefulness of a forecast in minimizing the economic costs associated with protecting against the effects of bad weather and the losses incurred when bad weather occurs but the user did not take protective action. The improvement in economic value of the forecast is measured relative to that of a climatology forecast and usually plotted as a function of the cost/loss ratio. For probabilistic forecasts the curve of interest is actually an envelope of curves representing each of the probability values allowed by the forecast (in this case, 0.0, 0.1, 0.2, ... 1.0),

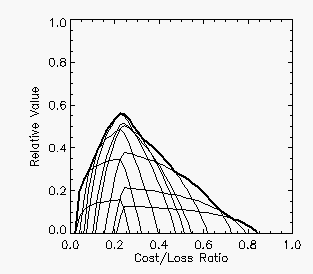and this envelope may look quite lumpy. The relative value curve shown here for the 24-hour POP forecasts is a case in point. The lighter curves represent the relative value as a function of cost/loss ratio using each of the probabilities as a yes/no threshold for the forecast, while the heavy curve is the outer envelope representing the maximum relative value possible. The maximum relative value of 0.57 occurred for a moderate cost/loss ratio of 0.23, which is the climatological frequency of rain in the sample. This plot shows that the POP forecasts have value for all decision makers except those with very low cost/loss ratios (who would always protect) or very high cost/loss ratios (who would never protect).

All of the plots and statistics shown so far have only considered the two-category cases of rain/no rain or heavier rain/not heavier rain. A summary score that takes multiple categories into account is the ranked probability score (RPS), which measures the closeness of the probability forecasts in all categories to the category in which the observation fell. For example, if the observation was in category 2, then a probability forecast for categories 0, 1, and 2 of [0.3, 0.6, 0.1] would score better than a forecast of [0.7, 0.2, 0.1] because the "weight" of the forecast was closer to the correct category. To put the ranked probability scores into context, the ranked probability skill score (RPSS) with respect to climatology is often used. For the year's worth of probability forecasts for Tampere the mean values of RPS, and the skill scores computed from these values, were:

	24-hour forecasts	48-hour forecasts
RPS	0.091	0.111
RPSS	0.222	0.069

According to the RPSS, and in agreement with the Brier skill scores, both the 24-hour and 48-hour forecasts were skillful.

Many thanks to Dr. Pertti Nurmi of FMI for providing these data and the photo of Tampere.

Back to Forecast Verification - Methods and FAQ Download IDL POP verification code for this example